FunOnFun

library(FunOnFun)
library(fdapace)
library(tidyverse)
#> ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
#> ✔ dplyr     1.1.4     ✔ readr     2.1.5
#> ✔ forcats   1.0.0     ✔ stringr   1.5.1
#> ✔ ggplot2   3.5.1     ✔ tibble    3.2.1
#> ✔ lubridate 1.9.3     ✔ tidyr     1.3.1
#> ✔ purrr     1.0.2     
#> ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ dplyr::lag()    masks stats::lag()
#> ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

Introduction

Welcome to the FunOnFun package! This package is designed to conduct multivariate functional Principal Component Analysis (MFPCA) on irregularly observed data. Let us generate some data:

Generate Data

Independence

set.seed(16)

n = 20
t = seq(0, 1, length.out = 50)
components = 2

mean_funs = list(
  function(t) -2*(t-0.5)^2 + 5,
  function(t) 3*(t-0.75)^3 - 5
  )

eigen_funs_list = list(
  list(
    function(t) sin(pi*t),
    function(t) cos(pi*t)
  ),
  list(
    function(t) sin(3*pi*t),
    function(t) cos(3*pi*t)
  )
)

lambdas = c(5, 3)

X = FunOnFun::simMFPCA(16, t, n, components, mean_funs, eigen_funs_list, lambdas, response = FALSE)

Dependent

mean_funs = list(
  function(t) 6*exp(-(t-1)^2),
  function(t) -2*14^(t-0.5)
)

eigen_funs_list = list(
  list(
    function(t) cos(5*pi*t),
    function(t) sin(5*pi*t)
  ),
  list(
    function(t) sin(3*pi*t),
    function(t) cos(3*pi*t)
  )
)

B = matrix(c(5, 6, 7, 8),
           nrow = components,
           ncol = components)

Y = FunOnFun::simMFPCA(16, t, n, components, mean_funs, eigen_funs_list, lambdas, response = TRUE, B = B)
sigma = 0.001
E = matrix(rnorm(2*length(t)*n, mean = 0, sd = sigma), n, 2*length(t))

Y$X = Y$X + E

Visualize

matplot(t(X$X), 
        type='l', 
        ylab='X(t)', 
        xlab='time', 
        main='Plot of predictor curves', 
        col=rgb(0,0,0,alpha=0.4))
matlines(apply(t(X$X), 1, mean),
         type='l',
         lwd=3,
         lty=1,
         col="red")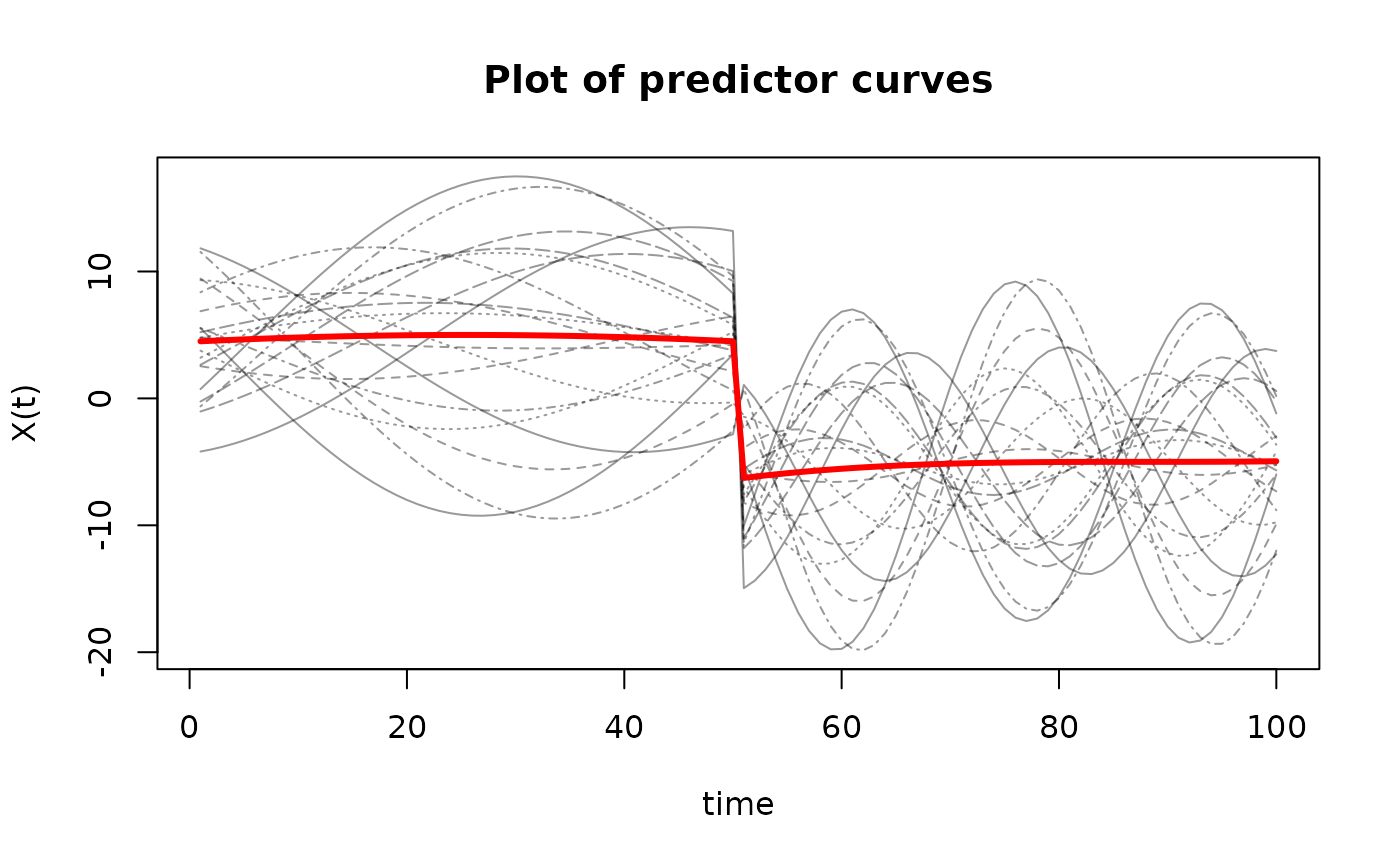

matplot(t(Y$X), 
        type='l', 
        ylab='Y(t)', 
        xlab='time', 
        main='Plot of response curves', 
        col=rgb(0,0,0,alpha=0.6))
matlines(apply(t(Y$X), 1, mean),
         type='l',
         lwd=3,
         lty=1,
         col = "red")

Simulate Irregular Missingness

X_miss = FunOnFun::simMiss(40, X$X, t, seed = 51)
Y_miss = FunOnFun::simMiss(40, Y$X, t, seed = 51)

Visualize Missingness

matplot(t(X_miss), 
        type='l', 
        ylab='X(t)', 
        xlab='time', 
        main='Plot of predictor curves with missingness', 
        col=rgb(0,0,0,alpha=0.4))
matlines(apply(t(X_miss), 1, mean, na.rm = T),
         type='l',
         lwd=3,
         lty=1,
         col="red")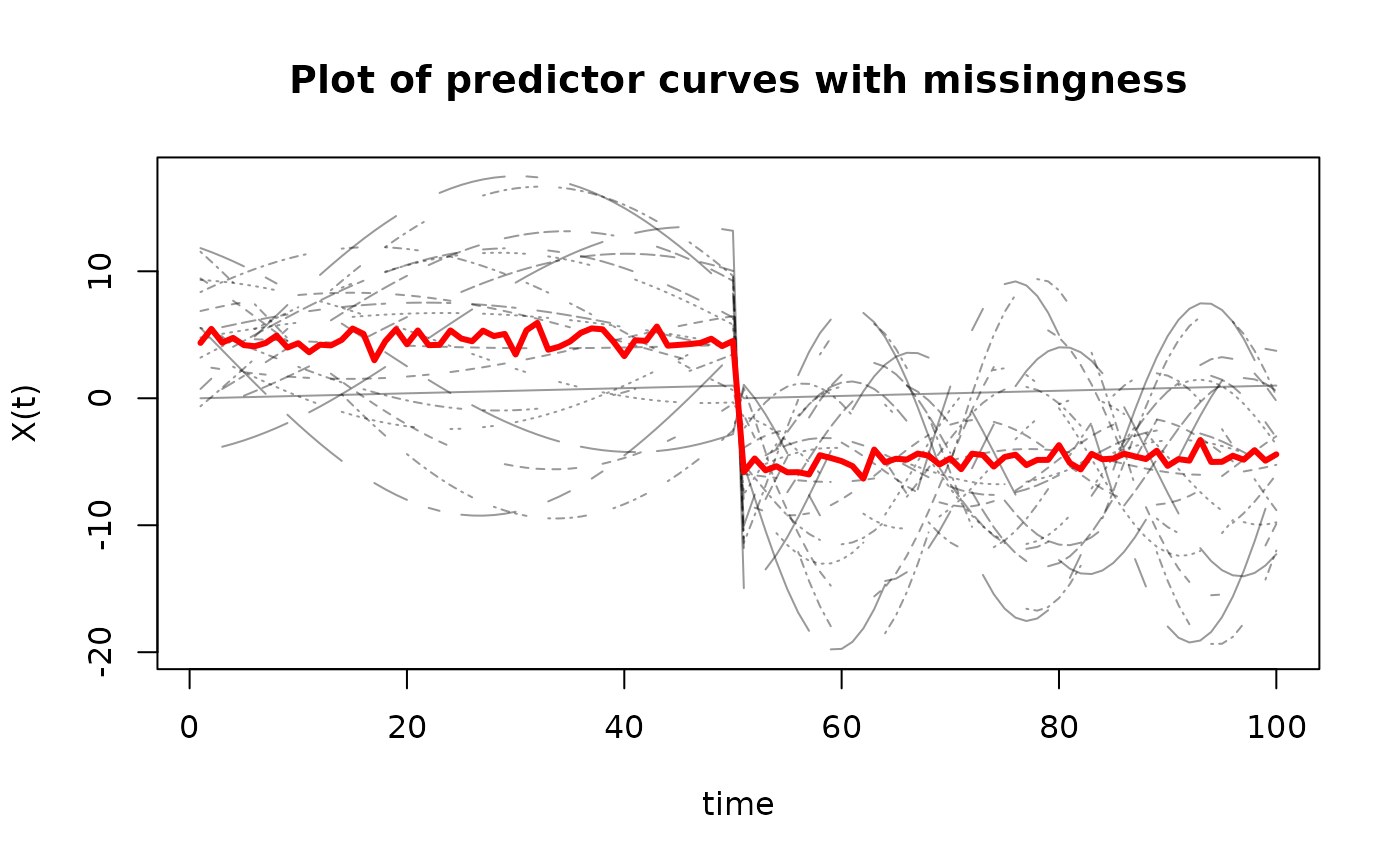

matplot(t(Y_miss),
        type='l', 
        ylab='Y(t)', 
        xlab='time', 
        main='Plot of response curves with missingness', 
        col=rgb(0,0,0,alpha=0.6))
matlines(apply(t(Y_miss), 1, mean, na.rm = T),
         type='l',
         lwd=3,
         lty=1,
         col = "red")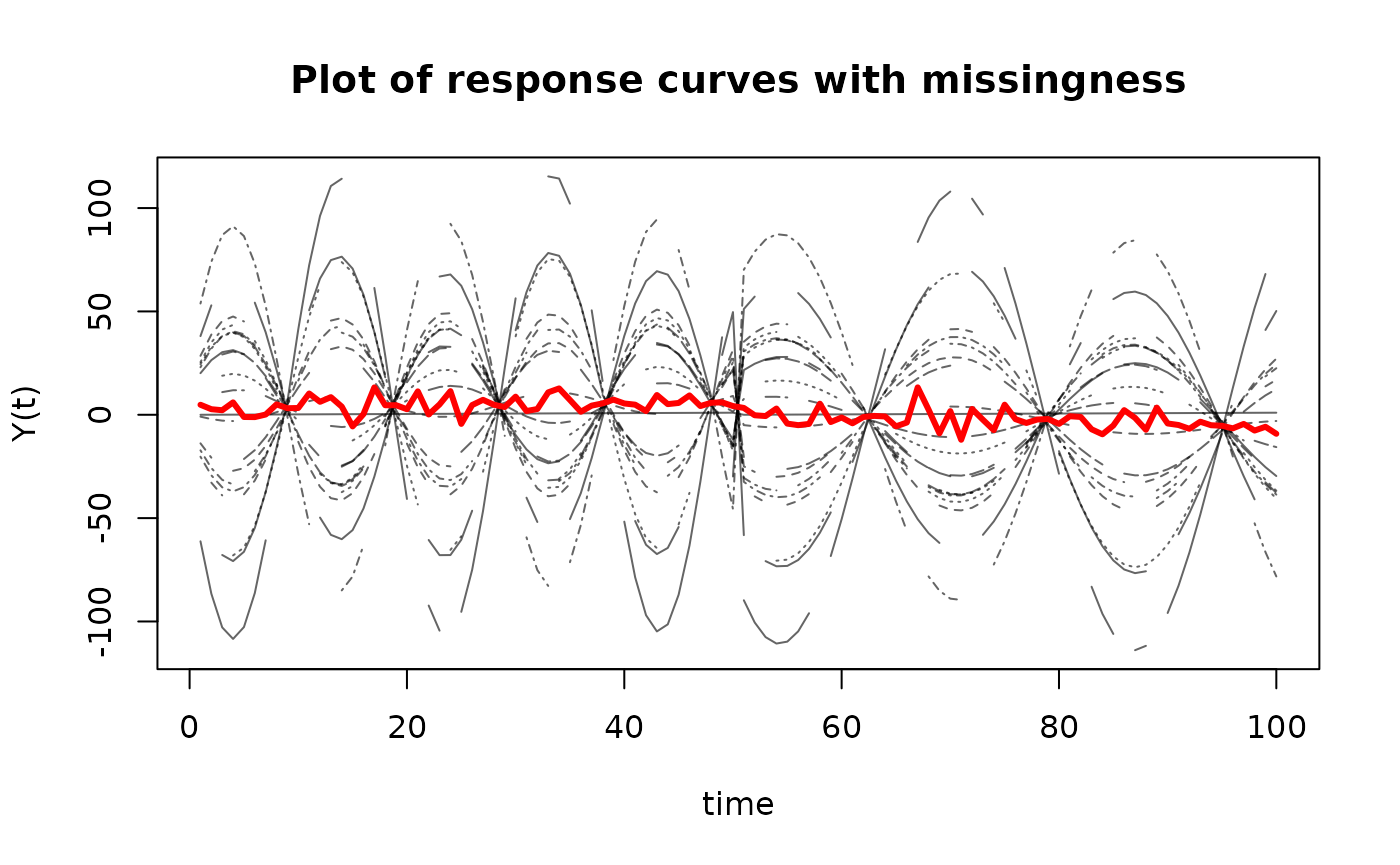

MFPCA

df = X_miss %>% FunOnFun::tibbleFormat(t) %>% FunOnFun::fpcaFormat(id_col = "id")
#> Registered S3 method overwritten by 'tsibble':
#>   method               from 
#>   as_tibble.grouped_df dplyr
df_Y = Y_miss %>% FunOnFun::tibbleFormat(t) %>% FunOnFun::fpcaFormat(id_col = "id")

Get Univariate FPCA Results

res_X1 = fdapace::FPCA(df$Variable1,
                       df$Time,
                       list(dataType = "Sparse",
                            error = F,
                            kernel = "epan",
                            verbose = F,
                            nRegGrid = length(t)))

res_X2 = fdapace::FPCA(df$Variable2,
                       df$Time,
                       list(dataType = "Sparse",
                            error = F,
                            kernel = "epan",
                            verbose = F,
                            nRegGrid = length(t)))

res_Y1 = fdapace::FPCA(df_Y$Variable1,
                       df_Y$Time,
                       list(dataType = "Sparse",
                            error = T,
                            kernel = "epan",
                            verbose = F,
                            nRegGrid = length(t),
                            methodSelectK = 2))
res_Y2 = fdapace::FPCA(df_Y$Variable2,
                       df_Y$Time,
                       list(dataType = "Sparse",
                            error = T,
                            kernel = "epan",
                            verbose = F,
                            nRegGrid = length(t),
                            methodSelectK = 2))

Run Irregular MFPCA

res = FunOnFun::irregMFPCA(components = 2,
                           split = T,
                           res_X1,
                           res_X2)

res_Y = FunOnFun::irregMFPCA(components = 2,
                             split = T,
                             res_Y1,
                             res_Y2)